Better Understanding How LEAPS Behave

LEAPS and the Greeks (UUP is used as a good example)

Long-term Equity AnticiPation Securities are options contracts that expire one or more years in the future. LEAPS trade just like regular calls and puts except the additional time to expiration (a) increases the time-premium component of their cost, and (b) increases their sensitivity to the Greeks Vega and Rho*.

So why trade LEAPS if they are more expensive than shorter-dated options?  One obvious answer is that the particular trade in question requires years to play out, such as the possible scenario we have with our current UUP trade which could take years. But why not just use shares and obviate the need to pay any premium at all?  Good question, LEAPS are often used by professionals in complex options strategies such as protective puts, collars, bull spreads and calendars. But for our purposes, we are using LEAPS to enhance our returns and limit our downside to the price paid for the contract.

I began as a small account trader and would use simple call (or put) LEAPS in lieu of shares to grow my account faster. For this strategy to work, the trader needs the change in the price of the underlying asset to be large enough to offset the extra premium paid for the LEAPS contract. If one is expecting a mere 10-20% change in the underlying asset, then naked call or put LEAPS are likely not the proper instrument to use. (Although exceptions to this exist if one isn’t planning to hold the LEAPS for too long, provided Vega is low. See below.) Importantly, the time-premium component of their cost is less of a concern than one might first expect due to the way time decay works.

Theta-Decay

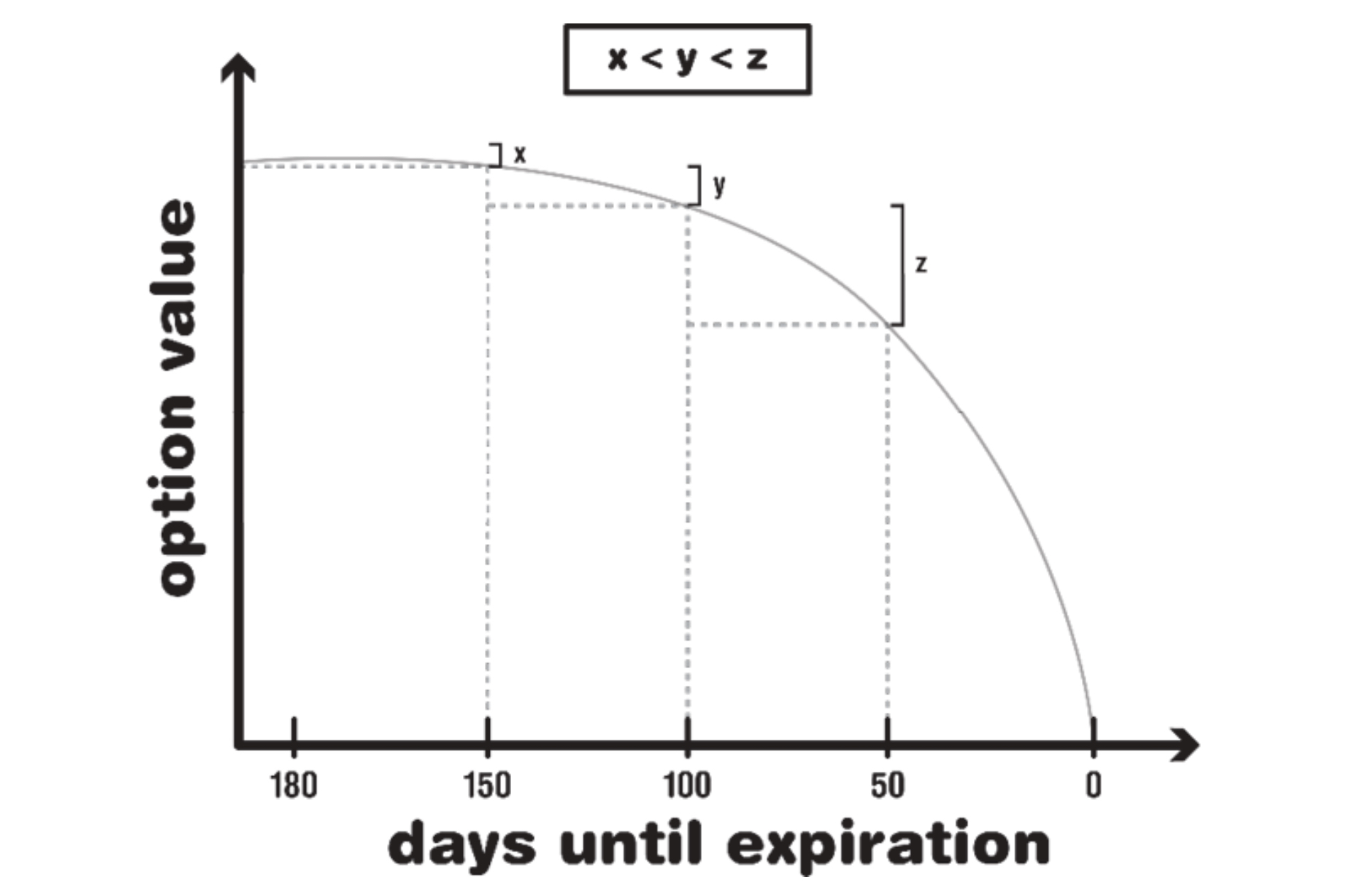
Theta is the Greek that measures the change in the price of an option as time passes. Theta is usually expressed as a negative number because if all other things remain equal (underlying price, interest rates, and volatility), an option will lose value as time passes, at an ever increasing rate.  Theta a measure of this (and varies for an at the money option in a way proportional to the inverse of the time remaining on the option squared). It’s intuitive to anyone who's ever traded options: the option’s value will decay over time, as expiration draws closer. This is called theta-decay. The important thing to remember is that time-decay increases more and more the closer we get to expiration. The decay starts off slow and speeds up exponentially:

 This chart illustrates that time decay is much less of a factor a year from expiration than it is even 100 days or 50 days from expiration. This allows us to use LEAPS in lieu of shares for a period of time before time decay becomes a large concern. Thus, it often pays to *not* hold a LEAPS contract to expiration. In other words, the slow onset of theta-decay mitigates some of the time premium concerns from trading options.

Now that we have addressed the largest drawback of using LEAPS, there is one other that needs to be mentioned.

 Vega

Options on an underlying asset with high implied volatility carry a higher premium than options on an underlying asset with low implied volatility. This is intuitive:  the more volatile the asset, the more expensive the option.  For exampe, if an instrument’s price is expected to swing wildly, then it has more likelihood to be in the money at expiration and thus its seller will demand more for it. 

Not a Greek letter (someone, sometime, will have to explain to me how Vega got its name), Vega measures the effect on an options’s price from a 1% change in its implied volatility.  All options have some level of Vega. An option with high Vega will be more susceptible to changes in implied volatility than an option with low Vega. LEAPS may have a temporary reprieve from the worst effects of theta-decay, but they carry Vega.

When the SPX rises, its implied volatility (VIX) typically comes down. I’m not going to get into puts, hedging, fear, and psychology but just stating a fact all traders know: as the price of an instrument continues to rise, its implied volatility typically comes down.  As explained in the previous paragraph, options with lower implied volatility carry less premium. Thus, as the implied volatility of an option comes down, so does its price. For call options, this means as price continues to rise on the underlying (increasing price via some combination of Delta and Gamma), there will be an opposing downward force on price because its implied volatility is decreasing; this is Vega.   

The UUP calls are a good example of this. This past week (Monday – Thursday), UUP rose 2.5% from 27.3 to 27.97.  All things being equal, this quick of a rise in price should have increased the value of our options but it didn’t. They remained relatively unchanged in the $1.35 range those 4 days. Why? Because UUP LEAPS carry Vega and the implied volatility of the instrument came down enough to cancel out the price appreciation.

Then, on Friday, UUP fell back down to 25.57 and implied volatility on UUP shot up.  The result: implied volatility increased enough to increase the price of our options by 15% 😮, to $1.55, despite a 1.4% sell-off in the underlying. This is Vega overpowering Delta, and something that we should expect moving forward when the implied volatility of the dollar index changes. (TL;DR) for small enough changes in the underlying price, a change in implied volatility can overpower the price appreciation of an option but for large enough moves in the underlying, Vega becomes more negligible. (Notice that if we owned puts, Vega would typically work in our favor.)

In conclusion, this was a fun exercise and a good illustration of how the lesser-known “Greeks” can affect options prices, specifically LEAPS. The Greeks not mentioned, Delta and Gamma, also deserve a write-up. But hopefully reading this has given you a pretty decent understanding of Theta, Vega, and Rho.

*Rho, arguably the least relevant Greek to options prices, attempts to quantify the affect of interest rates (from US Treasuries) on the cost of an option. For example, a two year LEAPS option would compare to a 2YR US Treasury, and as 2YR treasury rates change, so does the (tiny) affect they have on option’s price; Rho measures this. That’s pretty much all one needs to know about Rho.